摘  要  对金属材料中二相颗粒空间分布均匀性的各种定量金相分析方法进行了论述，并对网格计数法、截距法、面积法和区域法建立了统一计算表达式。通过实例讨论了各种均匀度定义分析法的差异，指出实际应用时应注意的问题。

1.前言

      金属材料二相组织在基材中的空间分布规律对材料的各项性能有很大关系，如石墨铸铁中的石墨颗粒分布，易切削钢硫化物的分布，弥散析出强化材料中弥散析出粒子的分布等。尤其在复合材料中，增强性材料在基体的分布情况尤为重要。因此有必要对材料中二相分布的均匀性进行定量描述和表征。

      近年来，随着计算机技术和体视学的发展，图像分析仪被广泛地应用于金相分析中，使传统的金相分析技术从定性或半定量的工作状态逐步向定量金相分析方向发展。因此使得对材料中二相分布的均匀性进行定量描述和表征成为可能。

      当前大多数金相分析标准都建立在传统的金相分析技术上，采用标准图谱进行比对评级，目前尚无有关分布均匀性定量的评定标准。我们知道，二相空间分布的均匀性反应在金相分析面上是组织截面分布的疏密程度，由于大多数有关二相分布均匀性的分析都是有关颗粒的或类似于颗粒分布的。因此我们这里主要讨论颗粒分布均匀性的定量金相分析方法，事实上，当二相组织截面为其它形态在基体弥散分布时，我们可以把它转换为金相分析面上的一个点（点或质心点），可作同样的讨论。

2.颗粒均匀度计算法

2.1网格计数法

      克里斯琴森（christiansen）对喷灌均匀度提出了一个用均匀系数来描述喷灌水量的均匀性[1]，这里我们借用其公式，并给予不同的物理意义：

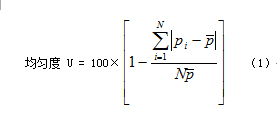
      它可以很好地表示在金相观察面上颗粒分布的均匀程度。具体做法是在金相照片上均匀分割 个网格，用图像分析仪分析每个网格的计数，或观察 个随机视域进行定量计算。

2.2截距法[2]

      上式的值可作为颗粒分布均匀性的描述和表征。

 

2.3面积法[3]

      与网格计数法相类似，求出 个均匀网格内或 个随机视域内颗粒的面积分数 （i = 1，… ）后，把网格计数法式中的 换成 即可：

2.4区域法

      在一张颗粒分布的金相图上，每一颗粒我们可以把它看成是二维空间的一个点。在每近邻两个点之间，作出它们的中垂线，直至和其它中垂线相交为止。这样，每个点就占据一个区域，区域的边界就是近邻点的中垂线。N个颗粒（点）就有N个区域，这样的区域我们称之为Dirichiet区[4]。图1是我们利用图像分析软件对石墨颗粒作出的Dirichiet区。图2是均匀分布颗粒由作图软件作出的模拟金相图，再由图像分析软件作出的Dirichiet区。

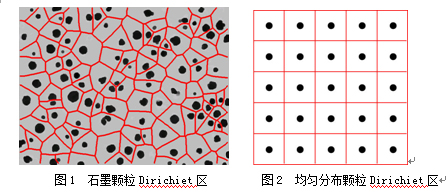
    颗粒分布的均匀性可以通过对Dirichiet区的分布特征（周长、边数和面积等）来分析描述。如果颗粒分布均匀，则Dirichiet区分布特征参数的标准偏差就会很小，如图2所示，均匀分布的颗粒每个颗粒所占据的Dirichiet区是一样的，其分布特征是相同的。

2.5独占圆法[5]

      东北林业大学罗传文教授对有限空间内，点空间分布均匀度作了理论上的探讨。在2维欧氏空间中，对一定空间范围内分布的点集，设任意一点与近邻体的距离为s，以s/2为半径所画的圆为该点的独占圆。根据定义，在一定边界内的点集，点集内所有独占圆是不重叠的，且两两相切。

设在一个长方形内有a×b = n个均匀分布的点，点与近邻体之间的距离均为s，称这样的格局为2维完全均匀格局。对均匀分布而言，独占圆面积的总和与点数无关，它总是长方形面积的π/4倍。由此得出格局均匀度定义：

3.实验与讨论

     为了实验间数据的比对，我们把上述四种计算方法（网格计数法、截距法、面积法、区域法），按数理统计的概念把它们统一起来，有利于相互间比较：

根据式（5），完全分布均匀的颗粒，其均匀度 U=1（100%），其它，U＜1。

在实际操作中，为充分体现样品的实际情况和检测精度，要有一定数量的分析视域。

以下均按式（5）计算。

3.1易切削钢硫化物均匀度测定

      易切削钢硫化物在基体空间的分布状态对其切削性能有很大影响，本工作分别用网格计

数法和面积法对同一张金相照片进行了硫化物分布均匀性的测定（图3）。照片均匀地被分割成9个网格区，对硫化物计数时采用坐标值。考虑到硫化物在边缘区会被网格线一分为二，影响计数的准确性，对每一网格区，凡在右下角和网格线相碰的硫化物不计数，而转入右下角网格区计数。但有可能造成有的硫化物坐标在上一区而转入下一区，这对于整张照片来讲，每个网格区是同等的。面积法利用灰度等级选定硫化物面积。

      测定结果见表一，一行为硫化物个数，二行为每个网格区硫化物的面积百分数。表格的位置和图3中被分割的区一一对应。按式(5)把表1数据代入，结果如下：

      网格计数法： 均匀度=78.8% ;  面积法：     均匀度=77.2%

     两者评定结果相近。

      网格计数法简单易行，缺点是不能反映颗粒间距离的影响，对于有规则偏聚的颗粒，无法作出正确的分析。另外，网格区的分割也要注意，尤其分析面总颗粒数不是很大时。在一个网格区内，它不能对均匀度作出判定。根据统计规律，网格区分割越多，相对精度也高一些，但增加了计算量。

面积法考虑了颗粒大小的影响，它和网格计数法在原理分析上是一样的。

3.2石墨颗粒均匀度测定

     我们对图1的石墨颗粒均匀度用四种方法（区域法、面积法、计数法、截距法）进行测定，结果如下：区域法： 均匀度=52%  面积法： 均匀度=84.5%   计数法：均匀度=86.8%   截距法:  均匀度=36% （9×7网格）；   34%（14×11网格）

     从以上结果看，面积法和计数法均匀度相近，而区域法计算结果和另外两种方法相差较大。区域法我们是对石墨颗粒Dirichiet区进行面积计算，图4是对图1隐去石墨颗粒后的Dirichiet区，它清楚地反映了各石墨颗粒在基体分布中所占据面积的大小。图5是Dirichiet区面积分布直方图，面积单位为像素点，它分布的均匀度确实不是很高。正如我们在上节所提出的那样，面积法和计数法不能很好地反映颗粒间距离的影响，而区域法对颗粒间距较敏感，每个Dirichiet区的分割，和颗粒间相互位置关系很大，其分布均匀性能较好地反映颗粒间的相互位置关系。另外我们注意到，区域法中Dirichiet区在分析面边缘有一定程度的影响，如果我们在分析计算时不予考虑，均匀度可能会有所改变。对图2均匀分布颗粒的模拟金相图，区域法算出的均匀度为97%，它反映了人工制作均匀分布颗粒模拟金相图时，颗粒分布肉眼不能区分的细微差异，若采用计数法和面积法，这种细微差异就难以反映。

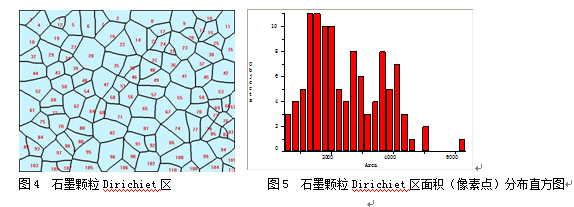
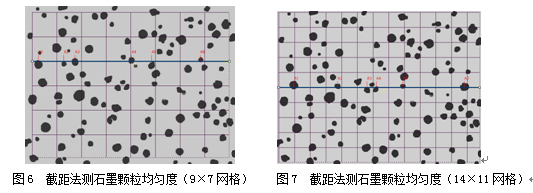
      在这四种方法中,截距法的评定值小,前一数据是9×7网格测得的截距计算的结果（图6），截距数35个，后一数据是14×11网格测得计算的结果（图7）, 截距数77个，两者相差不是很大。我们这里不列出每个颗粒间具体的截距值。一般来说，网格越多，截的颗粒也多，精度也较高，尤其颗粒较为稀疏情况下。和区域法一样，截距法对颗粒的间距较敏感，它们的差别在于截距法是纵横方向一维线上分布的分析, 区域法是二维面上分布的分析。

4.结论

    讨论和分析了现有颗粒分布均匀性评定的定量金相部分分析方法。归纳和建立了统一的，现有定量金相可操作的计算式。由于理论上、技术上和方法上的原因，目前尚无公认的优分析方法，也无可依的金相评定标准。在作颗粒分布均匀性评定时，我们可采用多种分析计算方法，以便对颗粒分布均匀性进行综合评估。每种检验法，它的侧重面（表征颗粒分布均匀性的特征量）各不相同，因而对均匀性的评定值存有差异。我们作测定时，应说明采用的分析法和特征量。根据我们的实验分析，区域法更合理些。